Effect Size

Effect Size
























In statistics, effect size is a measure of the magnitude of a phenomenon or treatment effect. It indicates the strength of the relationship between two variables or the impact of an intervention.


Types of Effect Size


There are several different types of effect size measures, including:

 Standardized Mean Difference (Cohen's d): Compares the means of two groups standardized by the pooled standard deviation.

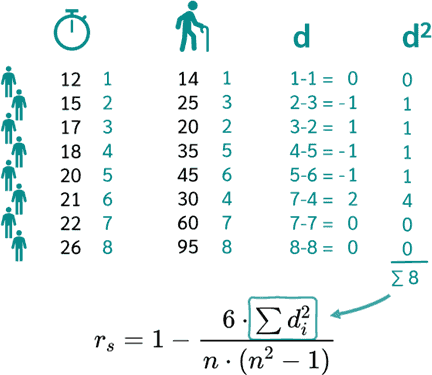
 Correlation Coefficient (Pearson's r, Spearman's rho): Measures the strength and direction of the linear relationship between two variables.

 Odds Ratio and Relative Risk: Measures the association between exposure and an outcome in epidemiological studies.

 Partial Eta Squared: Represents the proportion of variance in the dependent variable explained by a specific factor or treatment.


Importance of Effect Size


Effect size is important for a number of reasons:

 Complements statistical significance: Significance testing only indicates whether a result is statistically different from chance, but it does not provide information about its magnitude. Effect size measures quantify the strength of the effect.

 Compares different studies: Effect size allows researchers to compare the results of different studies, even if they used different sample sizes or methodologies.

 Guides sample size calculations: Effect size estimates can be used to determine the appropriate sample size for future studies.

 Supports clinical interpretation: In medical research, effect size can help clinicians assess the practical significance of a treatment or intervention.


Interpretation of Effect Size

The interpretation of effect size depends on the specific measure used and the context of the research. However, general guidelines suggest:


 Small Effect Size: 0.2 or less

 Medium Effect Size: 0.5 or less

 Large Effect Size: 0.8 or more


P-value vs Effect size


P-value


 Measures the likelihood of obtaining the observed results assuming the null hypothesis is true.

 Indicates statistical significance, but does not quantify the magnitude of the effect.

 A low p-value (<0.05) suggests that the observed results are unlikely to have occurred by chance alone.


Effect size

 Measures the magnitude of the observed effect.

 Provides a quantitative measure of how much the results deviate from the null hypothesis.

 Can be expressed as a difference between means, a correlation coefficient, or a regression coefficient.


Differences

 Statistical significance: P-value indicates statistical significance, while effect size does not.

 Magnitude of effect: P-value does not measure the magnitude of the effect, while effect size does.

 Interpretation: P-values alone can be misleading, as a statistically significant result does not necessarily imply a meaningful effect. Effect sizes provide a more informative interpretation of the results.


Importance

Both p-values and effect sizes are important for evaluating research findings:

 P-value: Ensures that the results are not due to chance alone.

 Effect size: Provides a meaningful measure of the effect and helps determine its practical significance.


Considerations

 The choice of p-value threshold (e.g., 0.05) is arbitrary and can affect the results.

 Effect sizes can vary depending on the sample size and the research design.

 Both p-values and effect sizes should be considered together for a comprehensive evaluation of research findings.

"Effect size helps readers understand the magnitude of differences found, whereas statistical significance examines whether the findings are likely to be due to chance. Both are essential for readers to understand the full impact of your work. Report both in the Abstract and Results sections"


Example 1:

Suppose a researcher conducts a study comparing two teaching methods. The study finds a statistically significant difference between the two methods, with students in the experimental group performing better than students in the control group. The standardized mean difference (Cohen's d) is 0.6.

This effect size would be considered a medium effect size, indicating a moderate difference between the two teaching methods. It suggests that the experimental method may have had a noticeable impact on student performance.


Example 2:

Scenario: A clinical trial is conducted to evaluate the efficacy of a new diabetes drug. The primary outcome is the change in glycated hemoglobin (HbA1c) levels from baseline to endpoint.

Effect Size: Cohen's d

Calculation:

Cohen's d = (Mean change in HbA1c in drug group - Mean change in HbA1c in placebo group) / Pooled standard deviation


Assumptions:

 The distribution of change in HbA1c levels is approximately normal in both the drug and placebo groups.
 The variances of change in HbA1c levels are equal in the two groups (i.e., homogeneity of variances).

Interpretation:

 Small effect: Cohen's d < 0.2
 Medium effect: 0.2 ≤ Cohen's d < 0.8
 Large effect: Cohen's d ≥ 0.8

Example Results:

 Drug group: Mean change in HbA1c = -1.0%
 Placebo group: Mean change in HbA1c = -0.5%
 Pooled standard deviation = 0.8%

Cohen's d = (-1.0% - (-0.5%)) / 0.8% = -0.625


Interpretation:

The effect size of the drug treatment is medium (Cohen's d = 0.625). This indicates that the drug is moderately effective in reducing HbA1c levels compared to placebo.


......................................................................................................


👉 For the data analysis, please go to my Youtube(Ads) channel to Watch Video (Video Link) in  

      Youtube Channel (Channel Link) and Download(Ads) video.


      💗 Thanks to Subscribe(channel) and Click(channel) on bell ðŸ”” to get more videos!💗!!



👉 For Powerpoint presentation slide(Ads), please help to fill a short information, Please click here
      (Survey Link) and Download(Ads) the presentation slides from Google Drive(G_drive link)

                                 ðŸ’“ Thanks for your completing the Survey 💗

                                💓 Thanks for visiting and sharing my Facebook Page ðŸ’—

..............................................................................................................






  1. STATA for dataset restructuring, descriptive and analytical data analysis
  2. SPSS for dataset restructuring, data entry, data check, descriptive, and analytical data analysis
  3. Epi-Info for building questionnaires, data check, data entry, descriptive, and analytical data analysis
  4. Epidata-Analysis for dataset restructuring, descriptive and analytical data analysis
  5. Epi-Collect for building questionnaires, remote data entry, mapping, and data visualization
  6. Epidata-Entry for building questionnaires, data check, data entry, and data validation

👉 ចុះឈ្មោះážĨលូវនេះនឹងទទួលបានតម្លៃពិសេស!ðŸĪĐ‼️

................................................................................................


☎️ Mobile Phone: (+855) - 96 810 0024
ðŸ“ģ Telegram: https://t.me/sokchea_yann
ðŸšĐ Facebook Page: Page
📎 Please join us: Telegram Channel
🌎 Please visit the website Thesis Writing Skill: Website
👎 Please follow us: https://www.tiktok.com/@sokcheayann999
ðŸ“Đ Please send an email to us: Email
ðŸĄ Address៖ #27B, Street-271, Street-33BT, Phsar Boeng Tumpon, Sangkat Boeng Tumpon, Khan  
                      Meanchey,  Phnom Penh, Cambodia.


                                                   ðŸ’– Thanks for your contribution!!! 💕

ABA Account-holder name: Sokchea YAN

ABA Account number: 002 996 999

ABA QR Code:


 





or tap on link below to send payment:

https://pay.ababank.com/iT3dMbNKCJhp7Hgz6


✌ Have a nice day!!! 💞





Comments

Post a Comment

Popular posts from this blog

  For bacteriology testing aimed at identifying and conducting Antimicrobial Susceptibility Testing (AST) for GLASS (Global Antimicrobial Resistance Surveillance System) priority pathogens , various reagents and supplies are typically required. Here's a list of essential reagents for such testing: 1. Culture Media: Nutrient Agar : For general cultivation of bacteria. Blood Agar : For growing fastidious organisms and detecting hemolytic activity. MacConkey Agar : For selective isolation of Gram-negative bacteria, particularly Enterobacteriaceae. Mannitol Salt Agar : For the selective isolation of Staphylococcus aureus . Chocolate Agar : Enriched medium for fastidious organisms like Haemophilus and Neisseria species. Cetrimide Agar : For selective isolation of Pseudomonas aeruginosa . XLD Agar (Xylose Lysine Deoxycholate) : For selective isolation of Salmonella and Shigella . 2. Gram Staining Reagents: ...
Read more

Citrobacter freundii

Image
1. What is Citrobacter freundii? Citrobacter freundii  is a species of facultative anaerobic Gram-negative bacteria belonging to the family Enterobacteriaceae. It is rod-shaped and typically measures 1-5 Ξm in length.  This bacterium is commonly found in soil, water, sewage, food, and the intestinal tracts of animals and humans 1 2 . 2. Transmission of Citrobacter freundii Citrobacter freundii  can be transmitted through: Direct contact : With contaminated surfaces or materials. Ingestion : Of contaminated food or water. Nosocomial transmission : In healthcare settings, particularly affecting immunocompromised patients 2 . 3. Epidemiology of Citrobacter freundii Citrobacter freundii  is widely distributed in the environment and is a common component of the gut flora.  It is considered an opportunistic pathogen, primarily causing infections in immunocompromised individuals, the elderly, and those with prolonged hospital stay...
Read more

Spearman's Rank Correlation Coefficient (ρ)

Image
 Spearman's Rank Correlation Coefficient (ρ) Definition: Spearmans' rank correlation coefficient is a non-parametric measure of the correlation between two variables that examines the relationship between their rankings, rather than their actual values. Formula: $$ρ = \frac{\sum{i=1}^{n} (ri - si)^2}{\sum{i=1}^{n} (ri^2 + si^2 - 1)}$$ where:  n is the number of paired observations  ri is the rank of the i-th observation in the first variable  si is the rank of the i-th observation in the second variable Interpretation:  -1 ≤ ρ ≤ 1  Ï = 1: Perfect positive correlation (rankings of both variables are exactly the same)  Ï = -1: Perfect negative correlation (rankings of the variables are exactly opposite)  Ï = 0: No correlation (no relationship between the rankings) Assumptions:  The data should be ordinal, i.e., their values represent ranks or positions.  The relationship between the variables should be monotonic, i.e., as one variable incr...
Read more